HashTable

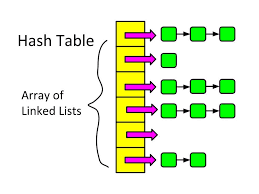
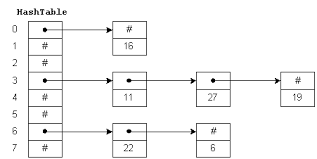
1. HashTable using Linked list

Hash tables are widely used to store and retrieve data efficiently. However, hash collisions are unavoidable.

In this assignment, you will implement a traditional hash table using separate chaining with linked lists to handle collisions.

You are not allowed to use Python built-in dictionaries (dict) or any hash table libraries.

Data Model

Attribute	Type	Description
key	string	Key used for hashing
value	any	Value associated with the key
next	Node	Reference to the next node in the bucket

Node Model

Component	Type	Description
table	list	Array of linked lists (buckets)
size	int	Number of buckets
count	int	Number of stored key–value pairs

Functions

Function	Description
hash_function(key)	Compute hash index from key
insert(key, value)	Insert or update a key–value pair
search(key)	Retrieve value by key
delete(key)	Remove key–value pair
display()	Show full hash table structure
load_factor()	Return current load factor

1. hash_function(key)

Convert a key into an index of the hash table.

Work in:

• Convert each character in the key into its ASCII value.
• Sum all ASCII values.
• Apply modulo operation with table size.

Input

Parameter	Type	Description
key	string	Key to be hashed

Output

Type	Description
int	Index in range [0, table_size - 1]

Ex:

hash_function("apple") => 3

2. insert(key, value)

Insert a new key–value pair into the hash table or update an existing key.

Work in:

1. Compute the hash index using hash_function(key).
2. Go to the linked list at that index.
3. Traverse the list:
   • If the key already exists => update its value.
   • Otherwise => insert a new node at the end of the linked list.
4. Increase element count if a new key is added.

Input

Parameter	Type	Description
key	string	Key to insert
value	any	Value associated with the key

Output

Type	Description
None	Prints insertion/update message

Ex:

Key 'apple' inserted at index 3
Key 'apple' updated at index 3

search(key)

Retrieve the value associated with a given key.

Work in:

1. Compute the hash index.
2. Traverse the linked list at that index.
3. Compare each node’s key with the search key.
4. Return value if found.

Input

Parameter	Type	Description
key	string	Key to search

Output

Type	Description
any	Value associated with the key
None	If key is not found

Ex:

Value for key 'banana': 20
Key 'orange' not found

delete(key)

Remove a key–value pair from the hash table.

Work in:

1. Compute the hash index.
2. Traverse the linked list at that index.
3. Track both current and previous nodes.
4. If the key is found:
   • Update pointers to remove the node.
5. Decrease element count.

Input

Parameter	Type	Description
key	string	Key to remove

Output

Type	Description
bool	True if deletion successful, False otherwise

Ex:

Key 'banana' removed from index 1
Key 'orange' not found

display()

Show the full internal structure of the hash table.

Work in:

• Iterate through each index of the table.
• Print the linked list stored at each bucket.
• Use arrows (->) to show chaining.

Output

Printed representation of the hash table.

Ex:

Hash Table:
[0] -> apple:10 -> mango:5
[1] -> banana:20
[2] -> empty
[3] -> grape:7

load_factor()

Measure how full the hash table is.

Work in:

• Divide number of stored elements by table size.
• load_factor = count / size

Output

Type	Description
float	Current load factor

Ex:

Load factor: 0.6

2. Student Record Management System Using Hash Table

Universities need to store and retrieve student records efficiently. Searching student information using linear data structures becomes slow when the number of students increases.

In this assignment, you will design a Student Record Management System using a Hash Table implemented with linked lists to handle collisions.

This system will allow fast insert, search, and delete operations based on a student ID.

You are not allowed to use Python built-in dictionaries or hash table libraries.

Data Model

Attribute	Type	Description
student_id	string	Unique student identifier
name	string	Student full name
major	string	Student major
next	Node	Pointer to next node in bucket

StudentRecordManagement class

Function	Description
hash_function(student_id)	Compute bucket index
add_student(id, name, major)	Insert or update student
find_student(id)	Retrieve student record
remove_student(id)	Delete student record
display_all()	Show entire hash table
load_factor()	Calculate load factor

Input Specification

The program processes user commands from standard input.

Add or Update Student

ADD <student_id> <name> <major>

Ex:

ADD S123 Alice ComputerScience

Output:

Student S123 added at index 2

or

Student S123 updated at index 2

Find Student

FIND <student_id>

Output:

Student Found:
ID: S123
Name: Alice
Major: ComputerScience

or

Student S999 not found

Remove Student

REMOVE <student_id>

Output:

Student S123 removed from index 2

or

Student S999 not found

Display All Students

DISPLAY

Output:

Hash Table:
[0] -> S101 -> S202
[1] -> empty
[2] -> S123 -> S305
[3] -> S450

Exit Program

EXIT

3. Assignment: String-Based Hash Table for Dictionary Lookup

Many real-world applications rely on string keys, such as usernames, URLs, email addresses, and dictionary words.

In this assignment, you will implement a hash table that uses string-based hash functions to efficiently store and retrieve words and their definitions.

Collisions must be handled using separate chaining with linked lists.

You are not allowed to use Python built-in dictionaries or hashing utilities.

Data Model

Attribute	Type	Description
word	string	Dictionary word (key)
meaning	string	Definition of the word
next	Node	Pointer to next node in bucket

Hash Table Structure

Component	Description
table	List	Array of linked lists
size	int	Number of buckets
count	int	Number of stored words

DictionaryLookup class

Function	Description
hash_function(word)	Compute hash index from string
insert(word, meaning)	Add or update word
search(word)	Find word definition
delete(word)	Remove word
display()	Show full hash table
collision_count()	Return number of collisions

Hash Function Specification (String-based)

Hash Formula:

hash = 0
for each character c in word:
    hash = (hash * 31 + ASCII(c)) % table_size

• 31 is a commonly used prime number
• ASCII(c) is the ASCII value of character c

Input Specification

The program reads commands from standard input.

Add or Update Student

ADD ADD <word> <meaning>

Ex:

ADD algorithm "a step-by-step procedure"

Output:

Word 'algorithm' inserted at index 4

or

Word 'algorithm' updated at index 4

Search Word

FIND <word>

Output:

Meaning of 'algorithm': a step-by-step procedure

or

Word 'algorithm' not found

Delete Word

REMOVE <word>

Output:

Word 'algorithm' removed from index 4

or

Word 'algorithm' not found

Display All Students

DISPLAY

Output:

Hash Table:
Hash Table:
[0] -> empty
[1] -> data["..."] -> structure["..."]
[2] -> empty
[3] -> queue["..."]
[4] -> algorithm["a step-by-step procedure"] -> array["a list"]

Exit Program

EXIT