Array-based Sequences - Queue, Stack

Queue

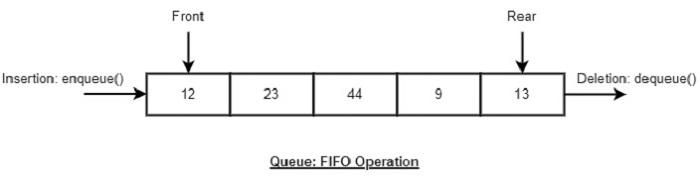
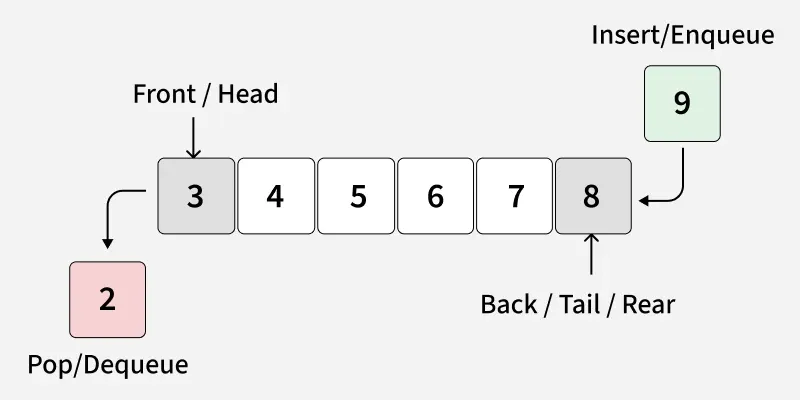
A Queue ADT stores arbitrary objects and follows the First-In, First-Out (FIFO) principle.

The first element inserted into the queue is the first one removed.

Queue Discipline (FIFO)

Term	Meaning
Front	Position where elements are removed
Rear (Back)	Position where elements are added

1.1 Abstract Data Type (ADT): Queue

Operation	Description
enqueue(x)	Insert element x at the rear
dequeue()	Remove and return the front element
peek() / front()	Return the front element without removing it
is_empty()	Check whether the queue is empty
size()	Return the number of elements

Exceptions: Attempting the execution of dequeue or front on an empty queue throws an EmptyQueueException

1.2. Object-Oriented Design of a Queue Class

1.2.1. Attributes

items: a container to store queue elements

1.2.2. Methods

• Constructor: init()
• Core operations: enqueue, dequeue
• Utility operations: peek, is_empty, size

1.3. Implementation 1: Queue Using a Python List

1.3.1. Array-Based Queue Implementation

A queue can be efficiently implemented using an array of fixed size N in a circular fashion.

Instead of shifting elements, the array is treated as circular, wrapping around when the end is reached.

Two integer variables are used to track the queue:

• f: index of the front element
• r: index immediately past the rear element

Important rule

• Array location r is always kept empty
• This helps distinguish between full and empty states

Array indices: 0  1  2  3  4  ...  N-1
Queue wraps around using modulo arithmetic

1.3.2. Size Operation

Algorithm size()
	return (N - f + r) mod N

Explanation:

• Computes the number of elements stored
• Works correctly even when indices wrap around

1.3.3. isEmpty Operation

Algorithm isEmpty()
    return (f = r)

Explanation:

• When f == r, the queue contains no elements

1.3.4. Enqueue Operation (Full Queue Case)

The enqueue operation inserts an element at position r

After insertion: r <- (r + 1) mod N

Algorithm enqueue(o)
	if size() = N <- 1 then
		throw FullQueueException
	 else  
		Q[r] <- o
		r <- (r + 1) mod N

In this case:

• enqueue throws an exception
• The specific exception type is implementation-dependent

1.3.5. Code Implementation

class Queue:
    def __init__(self):
        self.items = []

    def is_empty(self):
        return len(self.items) == 0

    def enqueue(self, item):
        self.items.append(item)

    def dequeue(self):
        if self.is_empty():
            raise IndexError("Queue is empty")
        return self.items.pop(0)

    def peek(self):
        if self.is_empty():
            raise IndexError("Queue is empty")
        return self.items[0]

    def size(self):
        return len(self.items)

1.3.6. Example Usage

Operation	Return Value	Queue (first <- Q <- last)
Q.enqueue(5)	–	[5]
Q.enqueue(3)	–	[5, 3]
len(Q)	2	[5, 3]
Q.dequeue()	5	[3]
Q.is_empty()	False	[3]
Q.dequeue()	3	[]
Q.is_empty()	True	[]
Q.dequeue()	“error”	[]
Q.enqueue(7)	–	[7]
Q.enqueue(9)	–	[7, 9]
Q.first()	7	[7, 9]
Q.enqueue(4)	–	[7, 9, 4]
len(Q)	3	[7, 9, 4]
Q.dequeue()	7	[9, 4]

Examples:

q = Queue()

q.enqueue(5)
q.enqueue(10)
q.enqueue(15)

print(q.dequeue())  # Output: 5
print(q.peek())     # Output: 10
print(q.size())     # Output: 2

Direct applications

• Waiting lists, bureaucracy
• Access to shared resources (e.g., printer)
• Multiprogramming

Indirect applications

• Auxiliary data structure for algorithms
• Component of other data structures

Array-based Queue

• Use an array of size N in a circular fashion
• Two variables keep track of the front and rear
  • f index of the front element
  • r index immediately past the rear element Array location r is kept empty

Queue Operations

• We use the modulo operator (remainder of division)

Algorithm size()
	return (N - f + r) mod N

Algorithm isEmpty()
	return (f = r)

• Operation enqueue throws an exception if the array is full
• This exception is implementation-dependent

Operation enqueue throws an exception if the array is full
This exception is implementation-dependent

1.3.7. Time Complexity Analysis (List-Based Queue)

Operation	Time Complexity	Explanation
enqueue	O(1)	Append to end of list
dequeue	O(n)	All elements shift left
peek	O(1)	Direct index access
is_empty	O(1)	Length check

Using list.pop(0) is inefficient for large queues.

1.4. Implementation 2: Efficient Queue Using collections.deque

Python provides deque (double-ended queue), optimized for FIFO operations.

1.4.1 Code Implementation

from collections import deque

class Queue:
    def __init__(self):
        self.items = deque()

    def is_empty(self):
        return len(self.items) == 0

    def enqueue(self, item):
        self.items.append(item)

    def dequeue(self):
        if self.is_empty():
            raise IndexError("Queue is empty")
        return self.items.popleft()

    def peek(self):
        if self.is_empty():
            raise IndexError("Queue is empty")
        return self.items[0]

    def size(self):
        return len(self.items)

1.4.2. Time Complexity (Deque-Based Queue)

Operation	Time Complexity
enqueue	O(1)
dequeue	O(1)
peek	O(1)

1.5 Comparison of Queue Implementations

Implementation	Pros	Cons
List-based	Simple, intuitive	Slow dequeue()
Deque-based	Fast, scalable	Requires import
Circular Queue	Memory efficient	More complex logic

2. Stack

An Abstract Data Type (ADT) is an abstraction of a data structure. It defines what operations are supported and how the data behaves, without specifying how the data is implemented.

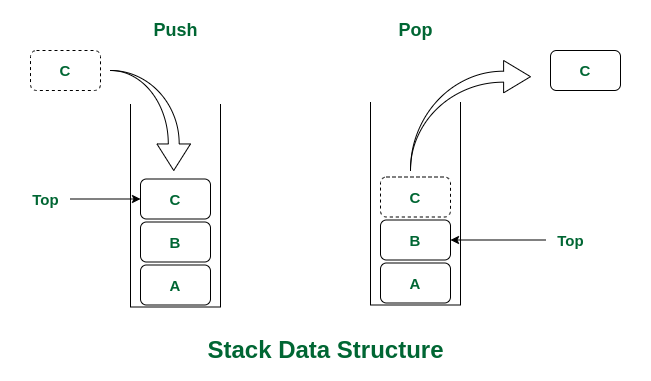
A Stack is a linear data structure that follows the LIFO principle: \(LIFO:Last-In, First-Out\)

This means:

• The last element inserted
• is the first element removed

An ADT specifies:

• Data stored
• Operations on the data
• Error conditions associated with operations

Example: ADT for a Stock Trading System

Data Stored: Buy and sell orders

Supported Operations

order buy(stock, shares, price)
order sell(stock, shares, price)
void cancel(order)

Error Conditions

• Buying or selling a nonexistent stock
• Canceling a nonexistent order

2.1 Basic Terminologies of Queue

A stack has one accessible end only, called the Top.

Term	Meaning
Top	Position where elements are added and removed
Bottom	The first element added

2.2 Abstract Data Type (ADT)

An Abstract Data Type (ADT) defines the behavior of a stack, independent of implementation.

Operation	Description
push(x)	Insert element x onto the top
pop()	Remove and return the top element
peek() / top()	Return the top element without removing it
is_empty()	Check if the stack is empty
size()	Return the number of elements

2.3. Object-Oriented Design of a Stack Class

2.3.1. Attributes

• items: container that stores stack elements

2.3.2 Methods

• Constructor: init()
• Core operations: push, pop
• Utility operations: peek, is_empty, size

2.4. Implementation 1: Stack Using a Python List

2.4.1. Code Implementation

class Stack:
    def __init__(self):
        self.items = []

    def is_empty(self):
        return len(self.items) == 0

    def push(self, item):
        self.items.append(item)

    def pop(self):
        if self.is_empty():
            raise IndexError("Stack is empty")
        return self.items.pop()

    def peek(self):
        if self.is_empty():
            raise IndexError("Stack is empty")
        return self.items[-1]

    def size(self):
        return len(self.items)

2.4.2. Example Usage

s = Stack()

s.push(10)
s.push(20)
s.push(30)

print(s.pop())    # Output: 30
print(s.peek())   # Output: 20
print(s.size())   # Output: 2

2.4.3. Time Complexity Analysis (List-Based Stack)

Operation	Time Complexity	Explanation
push	O(1)	Append to end of list
pop	O(1)	Remove from end
peek	O(1)	Direct index access
is_empty	O(1)	Length check

Very efficient using Python lists.

What’s happen? When:

• Occurs when pushing onto a full stack (bounded stack)
• Occurs when popping from an empty stack

2.5. Implementation 2: Bounded Stack (Optional Extension)

Application	Description
Function calls	Call stack in memory
Undo / Redo	Text editors
Expression evaluation	Postfix / Prefix
Syntax checking	Parentheses matching
DFS	Graph traversal

2.5.1 Implement Code

class BoundedStack:
    def __init__(self, capacity):
        if capacity <= 0:
            raise ValueError("Capacity must be a positive integer")

        self.capacity = capacity
        self.items = []

    def is_empty(self):
        return len(self.items) == 0

    def is_full(self):
        return len(self.items) == self.capacity

    def push(self, item):
        if self.is_full():
            raise OverflowError("Stack overflow: cannot push onto a full stack")
        self.items.append(item)

    def pop(self):
        if self.is_empty():
            raise IndexError("Stack underflow: cannot pop from an empty stack")
        return self.items.pop()

    def peek(self):
        if self.is_empty():
            raise IndexError("Stack is empty")
        return self.items[-1]

    def size(self):
        return len(self.items)

    def __str__(self):
        return f"Stack(bottom → top): {self.items}"

2.5.2. Using

stack = BoundedStack(3)

stack.push(10)
stack.push(20)
stack.push(30)

print(stack)        # Stack(bottom → top): [10, 20, 30]
print(stack.peek()) # 30

# Stack overflow
# stack.push(40)    # OverflowError

print(stack.pop())  # 30
print(stack.pop())  # 20
print(stack.size()) # 1

# Stack underflow
# stack.pop()
# stack.pop()       # IndexError

2.5.3. Time & Space Complexity

Operation	Time Complexity
push	O(1)
pop	O(1)
peek	O(1)
is_empty	O(1)
is_full	O(1)

3. Excercises

3.1. Applying the Queue Data Structure – Service Queue Management System

3.1.1. Problems

In many real-world service systems such as banks, public service centers, hospitals, and customer support offices, service requests are typically processed in a First In – First Out (FIFO) order.

Without a proper queue management mechanism:

• Customers may be served in the wrong order
• The waiting process becomes difficult to track
• It is impossible to evaluate system performance through statistics

Therefore, the problem is to design and implement a queue-based service management system that:

• Manages customers in the correct service order
• Simulates the service process
• Provides basic operational statistics

The system must operate in a console-based environment and must not use any database.

3.1.2. System Requirements

The system must support the following functions:

1. Add a customer to the queue
   • A new customer is added to the end of the queue
   • The service order must strictly follow the FIFO principle
2. Serve a customer
   • Remove and process the customer at the front of the queue
   • If the queue is empty, the system must display an appropriate message
3. View the next customer
   • Display the information of the customer at the front of the queue
   • The customer must not be removed from the queue
4. Display the entire queue: show all waiting customers in the correct order
5. System statistics
   • Total number of customers served
   • Number of customers currently waiting
   • Average waiting time (can be simulated)

3.1.3. Data Requirements

Attribute	Data Type	Description
id	int	Customer identifier
name	string	Customer name
service_type	string	Type of service
arrival_time	int or float	Arrival time

3.1.4. Technical Requirements

• The Queue data structure must be used collections.deque
• No database is allowed
• The program must run in the terminal
• The code must be well-structured and commented

3.1.5 Input / Output Specification

— Input —

Main menu:

===== SERVICE QUEUE MANAGEMENT =====
1. Add customer to queue
2. Serve next customer
3. View next customer
4. Display queue
5. Show statistics
6. Exit
===================================

Input for adding a customer:

Customer ID: 101
Customer Name: Nguyen Van A
Service Type: Payment
Arrival Time: 12.5

— Output —

When a customer is successfully added:

Customer added to queue successfully.

When serving a customer:

Serving customer:
ID: 101
Name: Nguyen Van A
Service Type: Payment

When viewing the next customer:

Next customer in queue:
ID: 102
Name: Tran Thi B
Service Type: Registration

When the queue is empty:

The queue is empty. No customer to serve.

When displaying the entire queue:

Current Queue:
1. ID: 102 - Tran Thi B - Registration
2. ID: 103 - Le Van C - Inquiry

When showing statistics:

Total customers served: 5
Customers waiting: 2
Average waiting time: 4.2 minutes

3.2. Applying the Stack Data Structure – Expression Processing System

3.2.1. Problems

In many areas of computer science such as compilers, calculators, and programming language interpreters, expressions (arithmetic or logical) must be processed in a specific order.

However, expressions written in infix notation (e.g. 3 + 4 * 2) are not easy for computers to evaluate directly because operator precedence and parentheses must be handled correctly.

The problem is to design a system that:

• Converts expressions from infix notation to postfix notation
• Evaluates postfix expressions correctly
• Uses the Stack data structure as the core mechanism

The system must be implemented as a console-based program without using any external libraries for expression evaluation.

3.2.2. Requirements

1. Input an infix expression
   • The expression may contain:
     • Integers
     • Operators: +, -, *, /
     • Parentheses: ( and )
   • Example: 3 + (4 * 5)
2. Convert infix expression to postfix notation
   • Use a stack to handle operators and parentheses
   • Operator precedence rules must be respected
3. Display the postfix expression: output the converted postfix expression as a string
4. Evaluate the postfix expression
   • Use a stack to compute the final result
   • Each operator must pop operands from the stack
5. Handle invalid expressions
   • Mismatched parentheses
   • Invalid characters
   • Division by zero
6. The system must use a Stack to store:
   • Operators during infix-to-postfix conversion
   • Operands during postfix evaluation
7. Stack operations required: push, pop, peek, is_empty

3.2.3. Input / Output Specification

—Input—

Main menu:

===== STACK EXPRESSION PROCESSOR =====
1. Enter infix expression
2. Convert infix to postfix
3. Display postfix expression
4. Evaluate postfix expression
0. Exit
=====================================

Example input:

Enter infix expression: 3 + (4 * 5)

—Output—

After converting infix to postfix:

Postfix expression: 3 4 5 * +

After evaluating postfix expression:

Evaluation result: 23

If the expression is invalid:

Error: Mismatched parentheses.

If division by zero occurs:

Error: Division by zero.