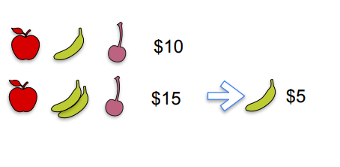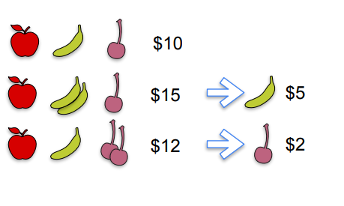Systems of Linear: three variables (3x3)

System of equations (3x3)

Quiz: Systems of equations

Problem 1: You’re trying to figure out the price of apples, bananas, and cherries at the store. You go three days in a row, and bring this information.

• Day 1: You bought an apple, a banana, and a cherry, and paid $10.
• Day 2: You bought an apple, two bananas, and a cherry, and paid $15.
• Day 3: You bought an apple, a banana, and two cherries, and paid $12.

  How much does each fruit cost?

System of equations 1:

\[\begin{cases} a + b + c = 10 \\ a + 2b + c = 15 \\ a + b + 2c = 12 \end{cases} \quad \Rightarrow \quad \begin{cases} a = 3 \\ b = 5 \\ c = 2 \end{cases}\]

System of equations 2 \(\begin{cases} a + b + c = 10 \\ a + b + 2c = 15 \\ a + b + 3c= 20 \end{cases} \quad \Rightarrow \quad \begin{cases} c = 5 \\ a + b = 5 \end{cases} \quad \Rightarrow \quad \begin{split} (0, 5, 5), (1, 4, 5), (2, 3, 5),... \\ \text{Infinitely many sols} \end{split}\)

System of equations 3 \(\begin{cases} a + b + c = 10 \\ a + b + 2c = 15 \\ a + b + 3c= 18 \end{cases} \quad \Rightarrow \quad \begin{split} \text{No solutions} \\ \text{From 1st and 2nd} \\ c = 5 \\ \text{From 2st and 3nd} \\ c = 3 \end{split}\)

System of equations 4 \(\begin{cases} a + b + c = 10 \\ 2a + 2b + 2c = 20 \\ 3a + 3b + 3c= 20 \end{cases} \quad \Rightarrow \quad \begin{split} \text{Infinitely many solutions} \\ \text{Any 3 numbers that ad to 10 work} \end{split} \quad \Rightarrow \quad (0, 0, 10), (0, 1, 9), (1, 1, 8),...\)

Singular vs non-singular matrices