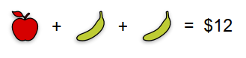Systems of Linear: two variables
Mermaid demo
I. Systems of Equations and Sentences
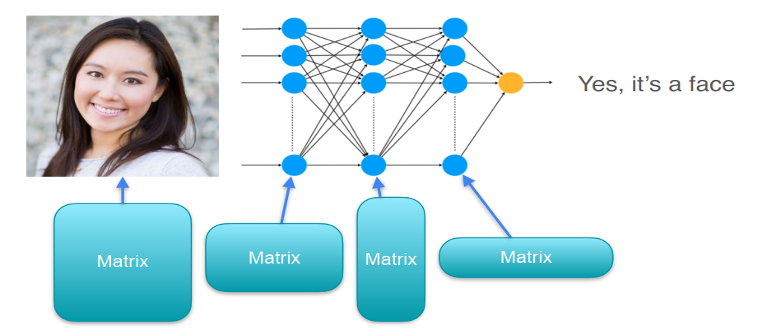
1. “Linear algebra is systems of linear equations.”
Trong ML, hầu hết các mô hình đều được mô tả bằng linear algebra:
- Input (features) ⇒ vector
- Parameters (weights) ⇒ vector/matrix
- Predictions ⇒ kết quả từ linear equations
Ví dụ:
\[y = w_1 x_1 + w_2 x_2 + \cdots + w_n x_n + b\]
That’s a systems of linear equations (Basic linear regression).
2. “When you think of equations, you think of sentences.”
- Một equation giống như một sentence trong ngôn ngữ: nó truyền đạt một thông tin về dữ liệu.
- Trong ML: mỗi phương trình biểu diễn một constraint (ràng buộc) hoặc một data point.
Ví dụ:
- Phương trình (Equation): 2x + y = 5
- Sentence: “Two apples and one banana cost 5 dollars.”
- Trong ML: Đây là một dữ liệu huấn luyện (x,y).
3. “Sentences that are giving you information about things in the world.”
- Trong ngôn ngữ: mỗi câu mô tả một sự thật.
- Trong ML: mỗi data point (sample) cũng là một “câu” về thế giới thực.
Ví dụ::
- Sentence 1: “Nam is taller than Lan.”
- Sentence 2: “Lan is 160 cm tall.”
⇒ We can infer: “Nam is taller than 160 cm.”
\[\begin{cases} A > B \\ B = 160 \end{cases} \quad \Rightarrow \quad A > 160\]4. “Systems of sentences behave a lot like systems of equations.”
- Ghép nhiều câu lại, ta hiểu rõ hơn bức tranh toàn cảnh.
- Trong ML: nhiều data points (training set) tạo nên một system of equations mà mô hình phải giải để tìm tham số phù hợp.
Ví dụ (linear regression với 2 điểm dữ liệu):
\[\begin{cases} 2x + y = 5 \\ x - y = 1 \end{cases}\]Giống như trong ML, bạn có nhiều mẫu huấn luyện, và bạn cần tìm nghiệm (weights) phù hợp với tất cả.
5. “Systems of sentences combine themselves to give you more information.”
- Khi các câu kết hợp, ta có thể suy ra điều mới.
- Trong ML, khi nhiều data points kết hợp, mô hình tổng quát hóa để đưa ra dự đoán cho dữ liệu chưa thấy.
Ví dụ:
- Training data (sentences):
- “If it rains, the ground gets wet.”
- “It is raining today.”
⇒ Kết hợp: “The ground will be wet today.”
Trong ML: mô hình học từ dữ liệu, rồi dự đoán cho input mới.
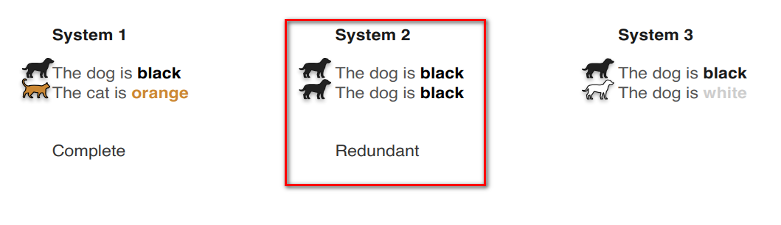
6. Example for system of sentences
Hệ thống này chứa nhiều thông tin như sentences và được gọi là a complete system.
The sentences lặp lại và do đó hệ thống này được gọi là dư thừa (redundant).
Hệ thống này được gọi là contradictory system vì con chó không thể vừa đen vừa trắng cùng một lúc, hãy nhớ rằng chúng ta có một con chó và nó chỉ có thể có một màu.
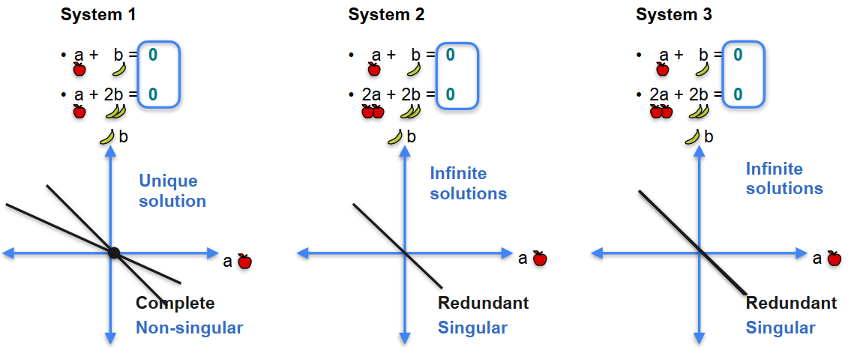
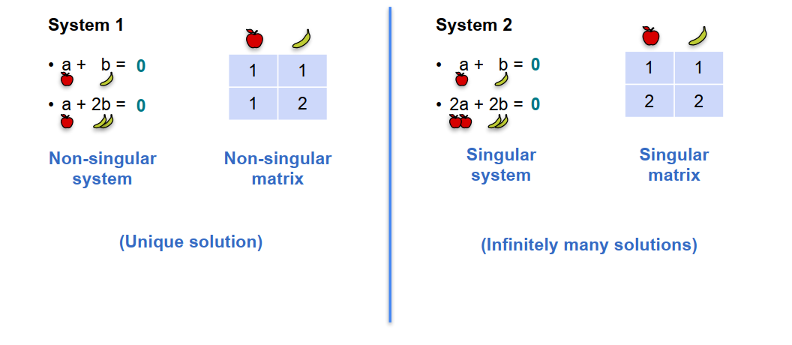
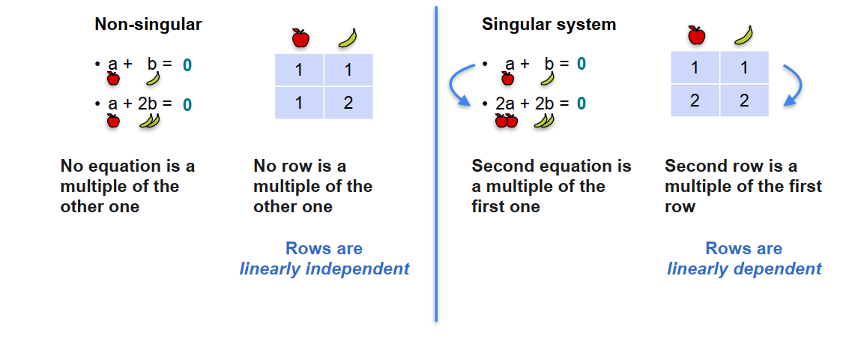
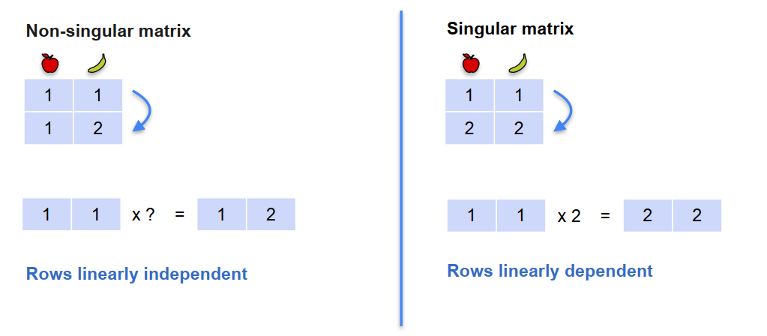
Non-singular: hệ có nghiệm duy nhất (complete system). Singular: hệ có vô số nghiệm (redundant system) hoặc hệ vô nghiệm (contradictory).
II. System of Linear Equations
1. From Sentences to Equations
Quy tắc chuyển đổi
- S1: Xác định thực thể (danh từ) → biến số cần tìm.
- S2: Chọn kiểu biến:
- Số thực / nguyên → biến x,y.
- Thuộc tính phân loại (màu, trạng thái) → mã hóa nhị phân (one-hot, 0–1).
- Logic/Boolean → biến nhị phân (0 hoặc 1).
- S3: Dịch quan hệ (động từ, số lượng) thành ràng buộc toán học:
- bằng (=),
- nhiều hơn / ít hơn (≥,≤)
- “một trong hai” → tổng bằng 1.
- S4: Thêm ràng buộc miền giá trị (ví dụ: số nguyên, không âm, nhị phân).
- S5: Phân tích hệ:
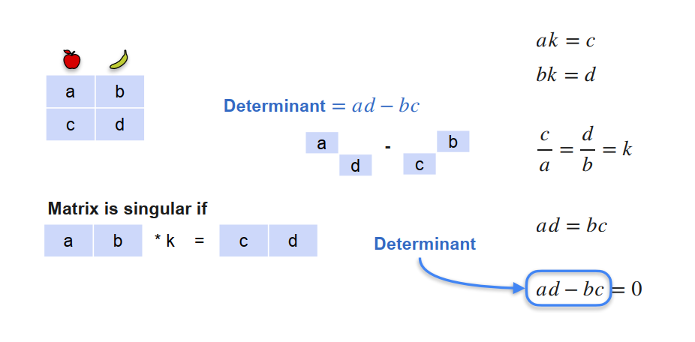
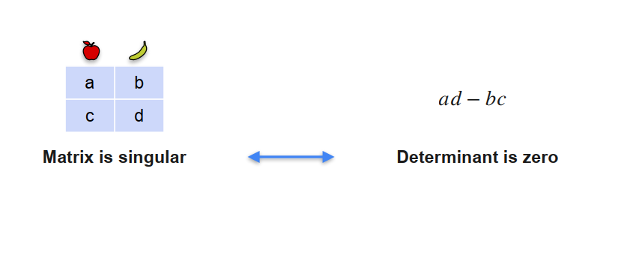
- Đủ phương trình, det(𝐴) ≠ 0 → nghiệm duy nhất.
- Thiếu phương trình hoặc ràng buộc dư thừa → vô số nghiệm.
- Mâu thuẫn → vô nghiệm.
1.1. Ví dụ 1
- Câu: “Between the dog and the cat, one is black”
- Câu: Each animal has only one color. \(\text{Each animal has only one color.} \quad \Rightarrow \quad d_B + c_B = 1\)
1.2. Ví dụ 2
.png)
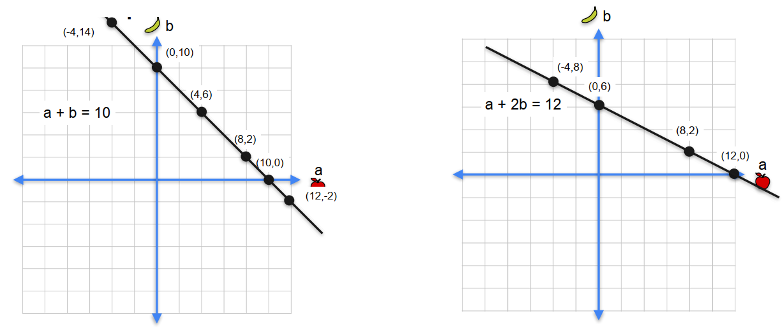
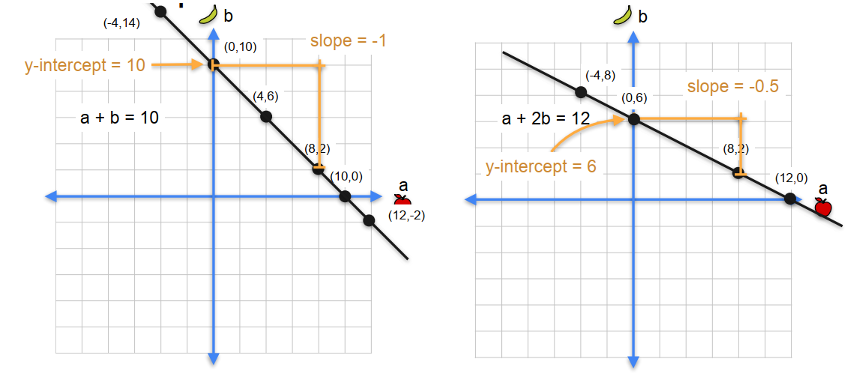
Câu: “The price of an apple an panana is $10”
- Biến số
- a = giá táo.
- b = giá chuối.
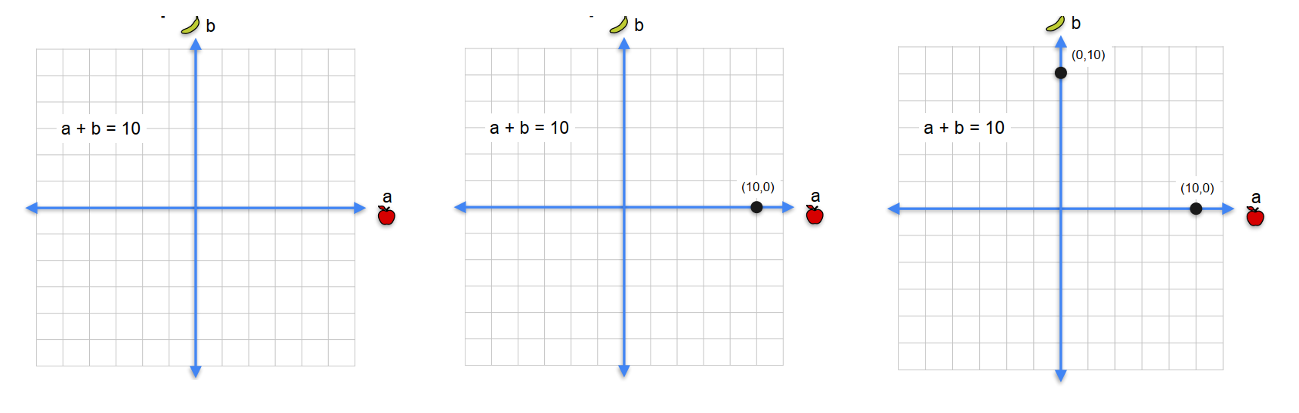
- Phương trình \(a + b = 10\)
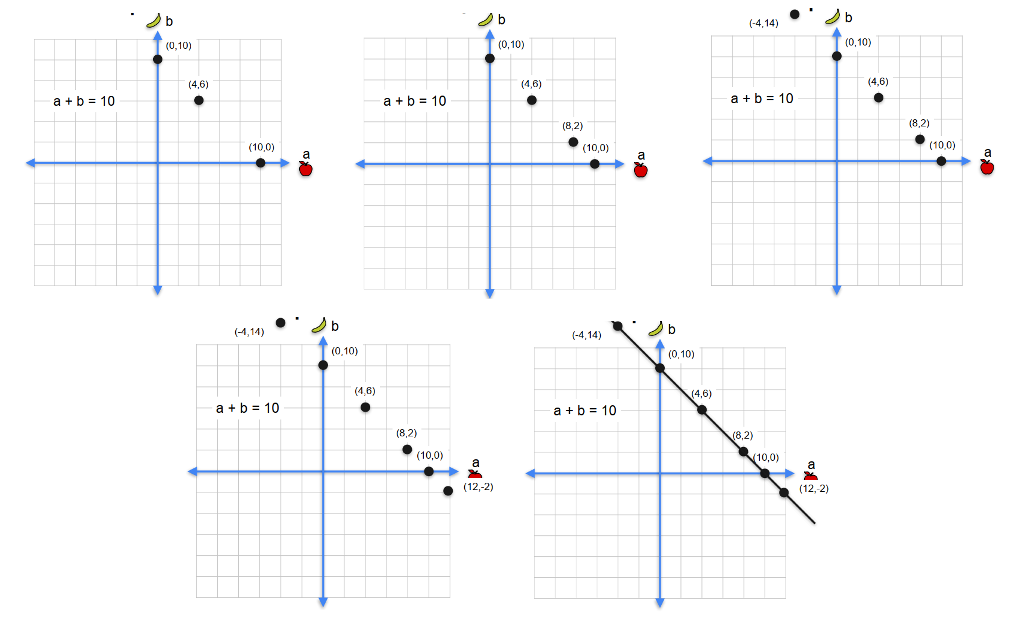
Một phương trình, hai ẩn → vô số nghiệm.
Ví dụ nghiệm:
- a = 6, b = 4
- a = 3.5, b = 6.5
- a = 10, b = 0
- … any pair summing to 10.
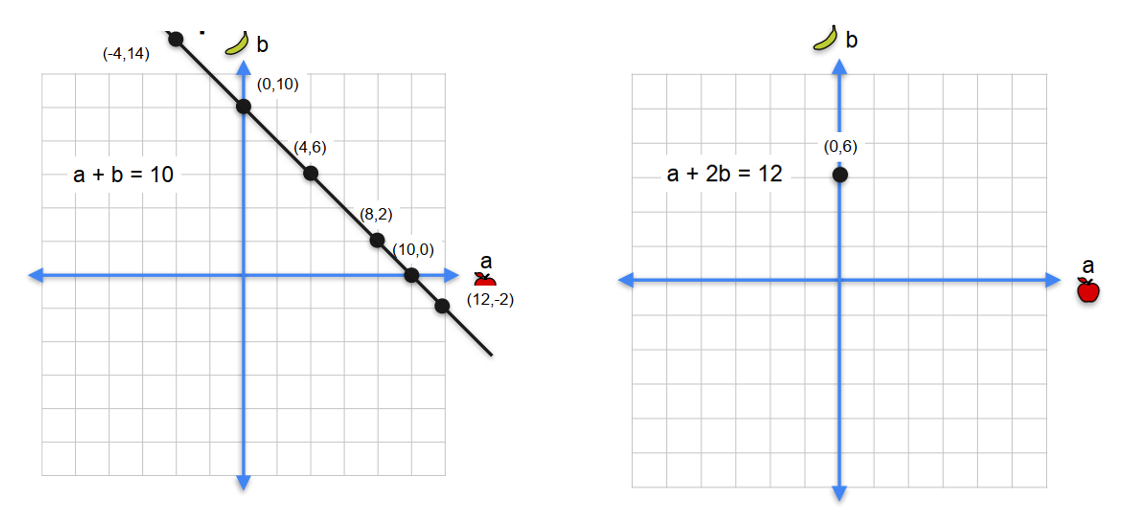
Bổ sung câu để đủ nghiệm duy nhất: “The apple costs twice the banana.” → a = 2b
\[\begin{cases} a + b = 10\\[4pt] a - 2b = 0 \end{cases} \quad\Rightarrow\quad \text{solve: } 2b + b = 10 \Rightarrow b=\tfrac{10}{3},\; a=\tfrac{20}{3}.\]1.3. Quizzes
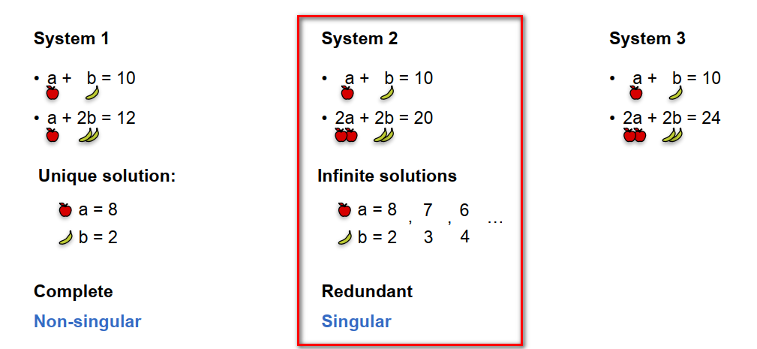
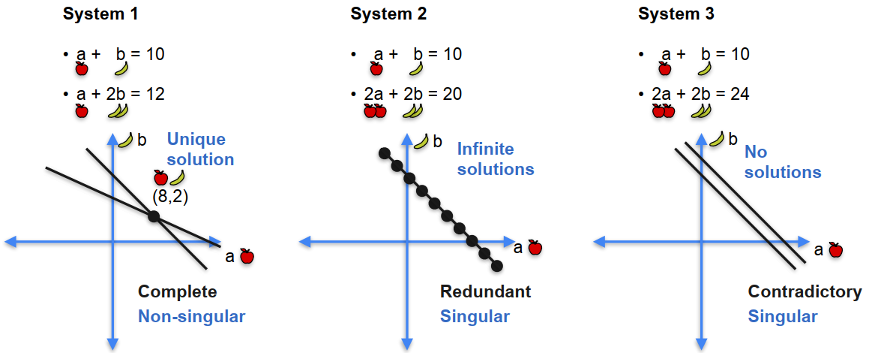
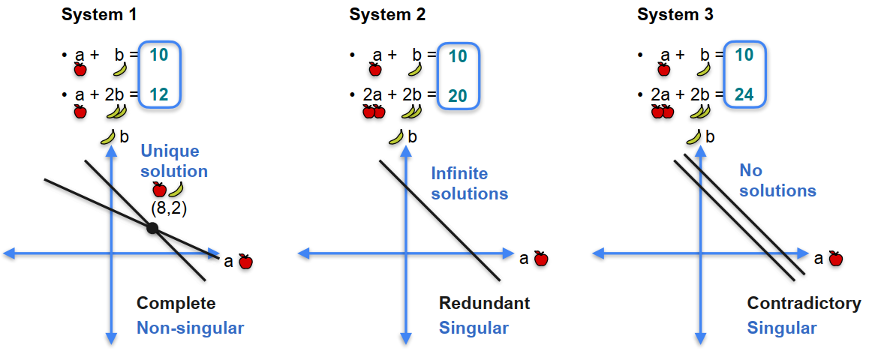
Quizz 1
You go two days in a row and collect this information:
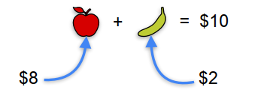
- Day 1: You bought an apple and a banana and they cost $10.
- Day 2: You bought an apple and two bananas and they cost $12.
Question: How much does each fruit cost?
Solution:
- Day 1: You bought an apple and a banana and they cost $10.
- Day 2: You bought an apple and two bananas and they cost $12.
- Solution: An apple costs $8, a banana costs $2.
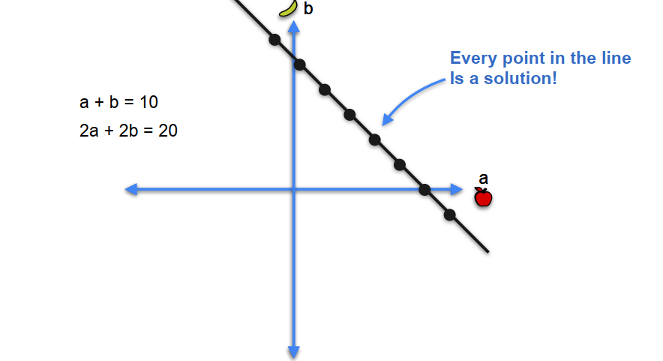
Quiz 2
You go two days in a row and collect this information:
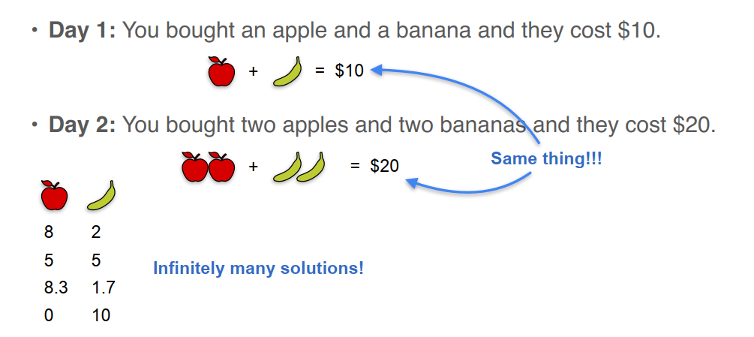
- Day 1: You bought an apple and a banana and they cost $10.
- Day 2: You bought two apples and two bananas and they cost $20.
Question: How much does each fruit cost?
- Day 1: You bought an apple and a banana and they cost $10.
- Day 2: You bought two apples and two bananas and they cost $20.
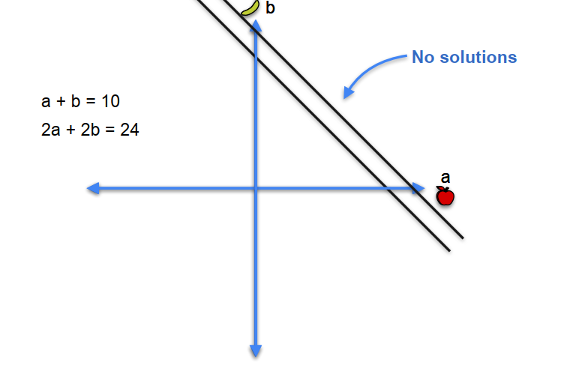
Quiz 3
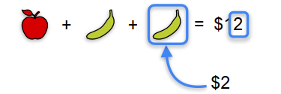
You go two days in a row and collect this information:
- Day 1: You bought an apple and a banana and they cost $10.
- Day 2: You bought two apples and two bananas and they cost $24.
Question: How much does each fruit cost?
2.2. Systems of equations
2.3. A linear equation
2.4. From Linear equation to line
2.5 Systems of equations as lines
A geometric notion of singularity
2.6 Singular vs nonsingular matrices
Linear dependence and independence
The determinant - Linear dependence between rows
The determinant
Determinant and singularity
