Table of contents

Python’s Sequence Types

In Python, a sequence is a collection of elements stored in a specific order. Each element can be accessed by its index.

Python provides several array-based sequence types, meaning the elements are stored contiguously in memory, like an array.

The most important ones are:

Type	Mutable?	Example
`list`	Yes	`[1, 2, 3]`
`tuple`	No	`(1, 2, 3)`
`str`	No	`"AI"`
`bytes`	No	`b'AI'`
`bytearray`	Yes	`bytearray(b'AI')`

An array can store primitive elements, such as characters, giving us a compact array.

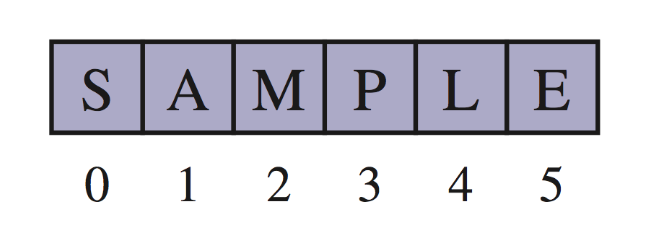
An array can also store references to objects.

Compact Arrays

1. What is a Compact Array?

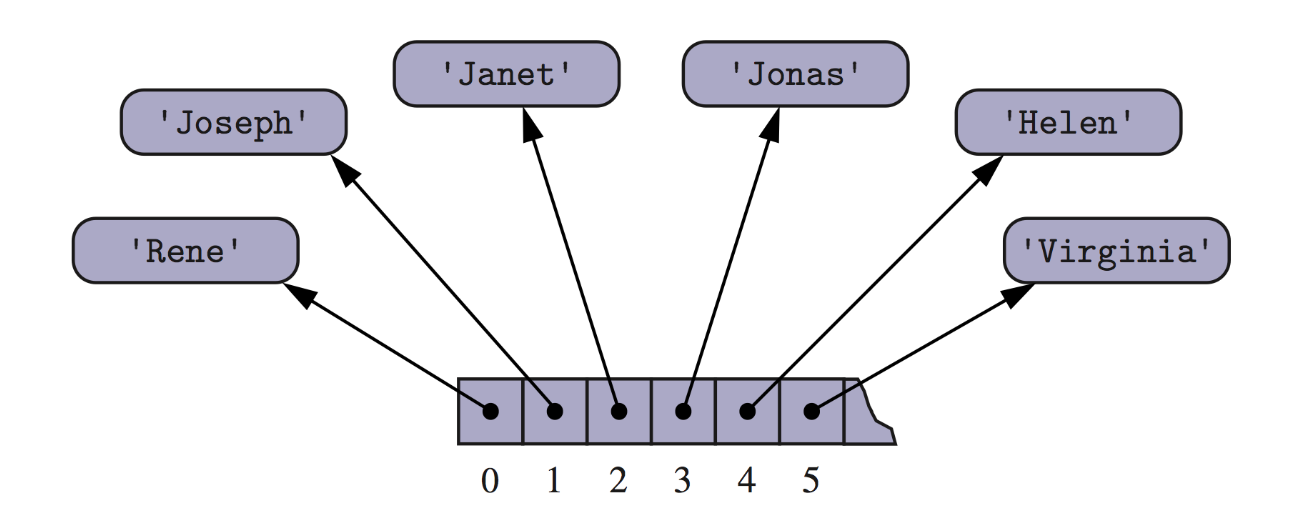
A compact array stores elements in raw binary form, just like arrays in C.

Primary support for compact arrays is in a module named array. That module defines a class, also named array, providing compact storage for arrays of primitive data types.

This makes them:

Much smaller in memory
Faster for numerical data
Restricted to one data type

Python implements this using:

from array import array

2. Creating an Array

The constructor for the array class requires a type code as a first parameter, which is a character that designates the type of data that will be stored in the array.

To create an array, you must specify:

A type code
An initial sequence of values

primes = array('i', [2, 3, 5, 7, 11, 13, 17, 19])

‘i’ = integer

[10, 20, 30, 40] = initial data

Accessing Elements:

print(primes[0])     # 2
print(primes[1:3])   # array('i', [3, 5, 7])

You can also modify them:

primes[0] = 99
primes.append(50)

3. Type Codes

The type code tells Python what kind of data the array will store.

Code	C Data Type	Typical Number of Bytes
‘b’	signed char	1
‘B’	unsigned char	1
‘u’	Unicode char	2 or 4
‘h’	signed short int	2
‘H’	unsigned short int	2
‘i’	signed int	2 or 4
‘I’	unsigned int	2 or 4
‘l’	signed long int	4
‘L’	unsigned long int	4
‘f’	float	4
‘d’	double (float)	8

array('f', [1.2, 3.4, 5.6])
array('i', [1, 2, 3, 4])

4.Compact Arrays vs Lists

Feature	List	array
Can mix types	Yes	No
Memory usage	High	Low
Speed for numbers	Slower	Faster
Numeric processing	OK	Better
Used in AI/data	Sometimes	Very common

When to Use array Instead of list

Use array when:
All values have the same type
You need high performance
Memory usage matters

Use list when:

Data types are mixed
You need flexibility

Insertion in an Array

Consider an array with n elements:

A = [A0, A1, A2, ..., A(n−1)]

We perform an operation:

add(i, o)

In an add(o) operation (without an index), we could always add at the end

When the array is full, we replace the array with a larger one

How large should the new array be?

Incremental strategy: increase the size by a constant c

Doubling strategy: double the size

Algorithm add(o)
	if t = S.length - 1 then A <- new array of size …
		for i = 0 to n-1 do
			 A[i] <- S[i]
		S <- A
	n <- n + 1
	S[n-1] <- o

Which means insert object o at index i.

What Happens During Insertion?

To insert at position i, we must:

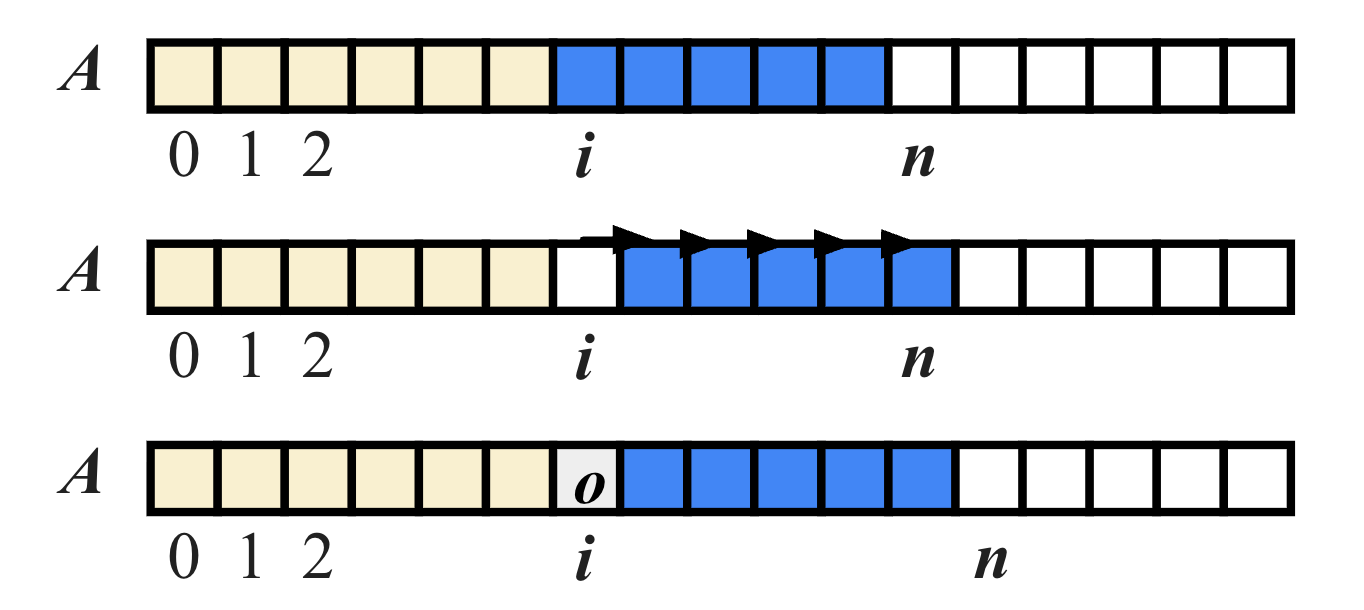
Step 1: Make space for the new element
Step 2: Shift all elements from index i to n−1 one position to the right

Notes:

list.append() is fast

list.insert(0, x) is slow

Why append() is fast

When you do:

lst.append(x)

Python:

Checks if there is free space at the end
If yes => stores x in the next empty slot
No elements need to move

So this is:

O(1) (constant time, on average)

Example:

[10, 20, 30, _]  => append(40)
[10, 20, 30, 40]

Even when Python runs out of space, it:

Allocates a larger block
Copies everything once
This happens rarely, so amortized time is still O(1).

Why insert(0, x) is slow

Now consider:

lst.insert(0, x)

You are inserting at the front.

Memory before:

[10, 20, 30, 40]

To put x at index 0, Python must:

Move 40 to index 4
Move 30 to index 3
Move 20 to index 2
Move 10 to index 1
Put x at index 0

Result:

[x, 10, 20, 30, 40]

Every element must be shifted one position to the right.

That is:

n moves for n elements => O(n)

Operation	What happens	Time
`append(x)`	Put `x` in next free slot	O(1)
`insert(0, x)`	Shift all elements right	O(n)

Element Removal in an Array

Assume we have an array with n elements:

A = [A0, A1, A2, …, A(n−1)]

We perform:

remove(i)

which means delete the element at index i.

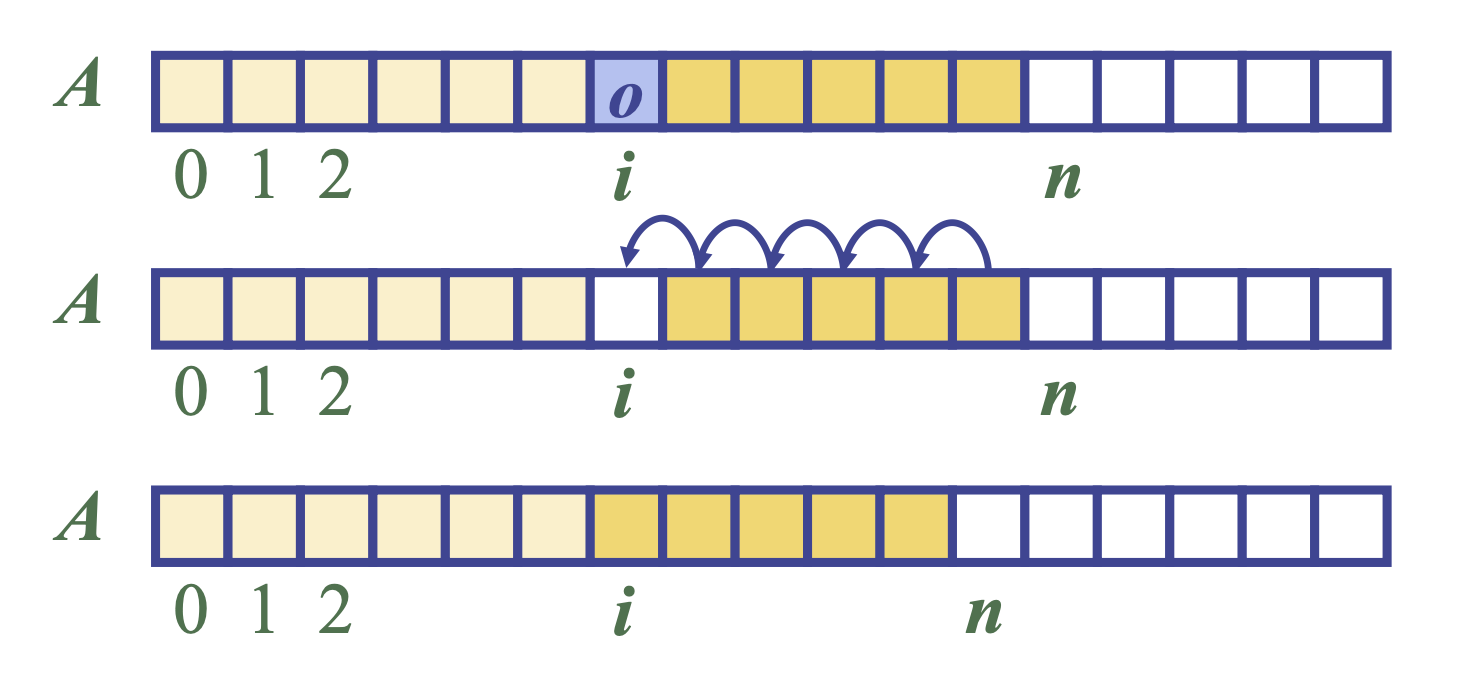
What Happens Internally?

When we remove A[i], we create a hole in the array:

Before: [A0, A1, A2, ..., A(n-1)]
remove(1) => remove A1
After hole: [A0,  _ , A2, A3, ..., A(n-1)]

To keep elements contiguous, we must shift everything after index i one position to the left:

A[i+1], A[i+2], ..., A[n−1]

Move to:

A[i], A[i+1], ..., A[n−2]

Final result:

[A0, A2, A3, ..., A(n-2)]

Performance of an Array-Based Dynamic List

In an array based implementation of a dynamic list:

The space used by the data structure is O(n)
Indexing the element at I takes O(1) time

Space Complexity

If the list stores n elements, it uses:

O(n) # space

Even though Python may allocate a little extra unused space, the memory grows linearly with the number of elements.

Indexing Time

Accessing an element:

A[i]  # Big-O: O(1)

This gives it very specific performance characteristics. Why?

Because the array stores elements in contiguous memory, so the address of A[i] is computed directly: address = base + i × element_size

Insertion and Removal

Operation	Worst Case Time	Reason
`add(i, x)`	O(n)	Elements must be shifted right
`remove(i)`	O(n)	Elements must be shifted left

Full code python

Operation	Time Complexity	Reason
`append(x)`	O(1) amortized	resize
`insert(i, x)`	O(n)	shift `n − i` elements
`remove(i)`	O(n)	shift `n − i − 1` elements
`A[i]`	O(1)	direct indexing

import ctypes    # provides low-level arrays

class DynamicArray:
    """A dynamic array class akin to a simplified Python list."""

    def __init__(self):
        """Create an empty array."""
        self._n = 0                         # count actual elements
        self._capacity = 1                  # default array capacity
        self._A = self._make_array(self._capacity)

    def __len__(self):
        """Return number of elements stored in the array."""
        return self._n

    def __getitem__(self, k):
        """Return element at index k."""
        if not 0 <= k < self._n:
            raise IndexError('invalid index')
        return self._A[k]

    def append(self, obj):
        """Add object to end of the array."""
        if self._n == self._capacity:
            self._resize(2 * self._capacity)
        self._A[self._n] = obj
        self._n += 1

    def insert(self, i, x):
        """Insert element x at index i."""
        if not 0 <= i <= self._n:
            raise IndexError('invalid index')

        # resize if array is full
        if self._n == self._capacity:
            self._resize(2 * self._capacity)

        # shift elements to the right
        for k in range(self._n, i, -1):
            self._A[k] = self._A[k - 1]

        self._A[i] = x
        self._n += 1

    def remove(self, i):
        """Remove element at index i."""
        if not 0 <= i < self._n:
            raise IndexError('invalid index')

        # shift elements to the left
        for k in range(i, self._n - 1):
            self._A[k] = self._A[k + 1]

        self._A[self._n - 1] = None  # avoid loitering
        self._n -= 1

    def _resize(self, c):
        """Resize internal array to capacity c."""
        B = self._make_array(c)
        for k in range(self._n):
            B[k] = self._A[k]
        self._A = B
        self._capacity = c

    def _make_array(self, c):
        """Return new array with capacity c."""
        return (c * ctypes.py_object)()

Exercises

1. User Activity Log Management

An AI-enabled system needs to store user activity logs in chronological order.

Each log entry is represented as a tuple:

(user_id, action)

Example:

("u01", "login")
("u01", "view_page")
("u01", "logout")

Task 1 – Add a Log Entry

This task simulates recording a new user action in the system.

New log entries should always be added to the end of the log list, preserving chronological order.

Create a function as below:

def add_log(logs, user_id, action):

Input:

logs: a DynamicArray object storing log entries
user_id: string representing the user identifier
action: string representing the user action

Output:

No return value
A new log (user_id, action) is appended to logs

Requirement

Use the append() method of DynamicArray

def add_log(logs, user_id, action):
    """
    Task 1: Add a log entry to the end of the DynamicArray.

    Input:
        logs    : DynamicArray
        user_id : str
        action  : str

    Output:
        None
    """
    logs.append((user_id, action))

Task 2 – Insert a Priority Log

Some system events (e.g., security checks) must be logged before all other events.

This task inserts a high-priority log at the beginning of the log list.

Create a function as below:

def insert_priority_log(logs, user_id, action):

Input:

logs: a DynamicArray object
user_id: string
action: string

Output:

No return value
A new log is inserted at index 0

Requirement

Use insert(0, x)

def insert_priority_log(logs, user_id, action):
    """
    Task 2: Insert a high-priority log at the beginning of the DynamicArray.

    Input:
        logs    : DynamicArray
        user_id : str
        action  : str

    Output:
        None
    """
    logs.insert(0, (user_id, action))

Task 3 – Remove an Invalid Log

Sometimes a log entry is incorrect or corrupted and must be removed.

This task deletes a log entry at a specified position while maintaining the order of remaining logs.

Create a function as below:

def remove_log(logs, index):

Input:

logs: a DynamicArray object
index: integer index of the log to remove

Output:

No return valueT
The log at position index is removed

Requirement

Use remove(index)

def remove_log(logs, index):
    """
    Task 3: Remove the log entry at the given index.

    Input:
        logs  : DynamicArray
        index : int

    Output:
        None
    """
    logs.remove(index)

Task 4 – Remove an Invalid Log

The system must be able to quickly retrieve a specific log entry for auditing or debugging purposes.

Create a function as below:

def get_log(logs, index):

Input:

logs: a DynamicArray object
index: integer

Output:

Returns the log entry at position index
Type: tuple (user_id, action)

Requirement

Use array indexing (logs[index])

def get_log(logs, index):
    """
    Task 4: Retrieve the log entry at the given index.

    Input:
        logs  : DynamicArray
        index : int

    Output:
        tuple (user_id, action)
    """
    return logs[index]

Using:

from dynamicArray import DynamicArray

# ... task 1
# ... task 2
# ... task 3
# ... task 4

logs = DynamicArray()

add_log(logs, "u01", "login")
add_log(logs, "u01", "view_page")
insert_priority_log(logs, "admin", "system_check")

print(get_log(logs, 0))
# ('admin', 'system_check')

remove_log(logs, 1)

Queue

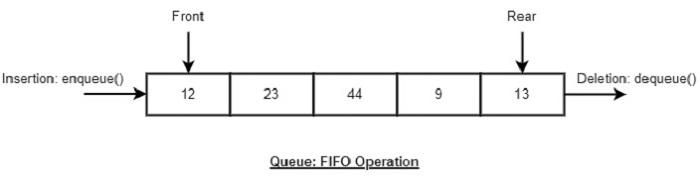
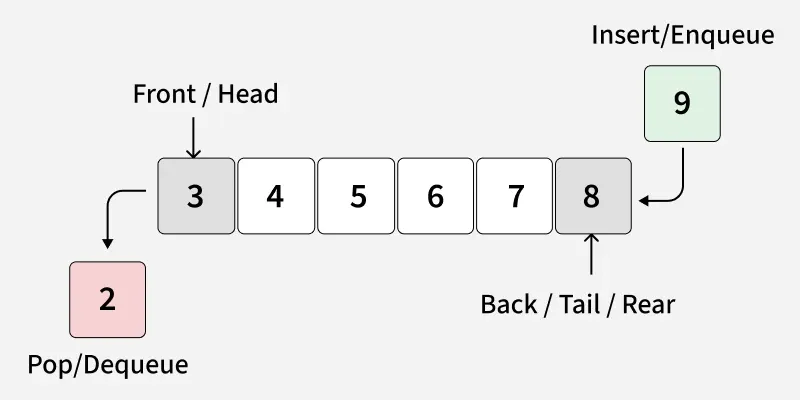
A Queue ADT stores arbitrary objects and follows the First-In, First-Out (FIFO) principle.

The first element inserted into the queue is the first one removed.

Queue Discipline (FIFO)

Insertion happens at the rear of the queue
Removal happens at the front of the queue

Main queue operations:

enqueue(object): inserts an element at the end of the queue
object dequeue(): removes and returns the element at the front of the queue

Auxiliary queue operations:

object first(): returns the element at the front without removing it
integer len(): returns the number of elements stored
boolean is_empty(): indicates whether no elements are stored

Exceptions: Attempting the execution of dequeue or front on an empty queue throws an EmptyQueueException

Time Complexity (Array-Based Queue)

Operation	Time
`enqueue`	O(1)
`dequeue`	O(n)
`first`	O(1)
`is_empty`	O(1)

Array-Based Queue Implementation

A queue can be efficiently implemented using an array of fixed size N in a circular fashion.

Instead of shifting elements, the array is treated as circular, wrapping around when the end is reached.

Two integer variables are used to track the queue:

f: index of the front element
r: index immediately past the rear element

Important rule

Array location r is always kept empty

This helps distinguish between full and empty states

Array indices: 0  1  2  3  4  ...  N-1
Queue wraps around using modulo arithmetic

Size Operation

Algorithm size()
	return (N - f + r) mod N

Explanation:

Computes the number of elements stored
Works correctly even when indices wrap around

isEmpty Operation

Algorithm isEmpty()
    return (f = r)

Explanation:

When f == r, the queue contains no elements

Enqueue Operation (Full Queue Case)

The enqueue operation inserts an element at position r

After insertion: r <- (r + 1) mod N

Algorithm enqueue(o)
	if size() = N <- 1 then
		throw FullQueueException
	 else  
		Q[r] <- o
		r <- (r + 1) mod N

In this case:

enqueue throws an exception
The specific exception type is implementation-dependent

Queue ADT function:

Operation	Return Value	Queue (first <- Q <- last)
Q.enqueue(5)	–	[5]
Q.enqueue(3)	–	[5, 3]
len(Q)	2	[5, 3]
Q.dequeue()	5	[3]
Q.is_empty()	False	[3]
Q.dequeue()	3	[]
Q.is_empty()	True	[]
Q.dequeue()	“error”	[]
Q.enqueue(7)	–	[7]
Q.enqueue(9)	–	[7, 9]
Q.first()	7	[7, 9]
Q.enqueue(4)	–	[7, 9, 4]
len(Q)	3	[7, 9, 4]
Q.dequeue()	7	[9, 4]

Direct applications

Waiting lists, bureaucracy
Access to shared resources (e.g., printer)
Multiprogramming

Indirect applications

Auxiliary data structure for algorithms
Component of other data structures

Array-based Queue

Use an array of size N in a circular fashion
Two variables keep track of the front and rear
- f index of the front element
- r index immediately past the rear element Array location r is kept empty

Queue Operations

We use the modulo operator (remainder of division)

Algorithm size()
	return (N - f + r) mod N

Algorithm isEmpty()
	return (f = r)

Operation enqueue throws an exception if the array is full
This exception is implementation-dependent

Operation enqueue throws an exception if the array is full
This exception is implementation-dependent

Stack

Abstract Data Type (ADT)

An Abstract Data Type (ADT) is an abstraction of a data structure. It defines what operations are supported and how the data behaves, without specifying how the data is implemented.

An ADT specifies:

Data stored
Operations on the data
Error conditions associated with operations

Example: ADT for a Stock Trading System

Data Stored: Buy and sell orders

Supported Operations

order buy(stock, shares, price)
order sell(stock, shares, price)
void cancel(order)

Error Conditions

Buying or selling a nonexistent stock
Canceling a nonexistent order

Basic Terminologies of Queue

Front: Position of the entry in a queue ready to be served, that is, the first entry that will be removed from the queue, is called the front of the queue. It is also referred as the head of the queue.

Rear: Position of the last entry in the queue, that is, the one most recently added, is called the rear of the queue. It is also referred as the tail of the queue.

Size: Size refers to the current number of elements in the queue.

Capacity: Capacity refers to the maximum number of elements the queue can hold.